Over a year ago, I wrote a blog post discussing the Additive Manufacturing (AM) equipment we have at Arizona State University (ASU), most of it part of a $2M (and since growing) investment at the Polytechnic School’s Innovation Hub. This post introduces a lesser-known aspect of our overall AM effort at ASU, and that is the curriculum around AM that we have developed rather organically over the past 2 years. Today, several students at ASU are stringing these courses together based on their interests, at the BS, MS and PhD levels. Over 200 students have enrolled in these courses so far.
Additive Manufacturing Courses
We have 5 courses at ASU that are specific to AM (i.e. they have AM in the title of the course). Two of these are offered in the Fall, and 3 in the Spring semester, as shown in Figure 1. Three different faculty members teach these courses, enriching the learning process with their own research and industry experiences.

- MFG 472: Additive Manufacturing (Instructor: Dhruv Bhate) This was the very first AM course developed at ASU and offered for the first time in 2015. Today the course has morphed into a flipped classroom format – students watch pre-recorded lectures and how-to videos, complete an online quiz, and classroom time is used for hands-on 3D printing. Students print parts in groups of 5 on six different 3D printing processes (see Figure 2) over a 12-week period (2 weeks per process). This includes build preparation, machine setup and post-processing and this year we also included metal 3D printing (on our Concept Laser MLab Laser Powder Bed Fusion system). This course serves as a hands-on introduction to AM and allows students to reflect on the different processes and their relative merits.

- MFG 598: Micro and Nano Additive Manufacturing (Instructor: Xiangfan Chen) In this course, first offered in the Fall of 2018, students learn the importance of AM at the micro- and nanoscales, and its role in development and innovation of micro-/nano-engineering. Students develop a rich knowledge of micro-/nanotechnologies, devices, capabilities, materials and applications. They explore the broad range of micro- /nano- AM applications, including biomedical, optical, consumer products, and creative artistry. And finally, they learn the latest trends and opportunities in micro-/nano- AM.
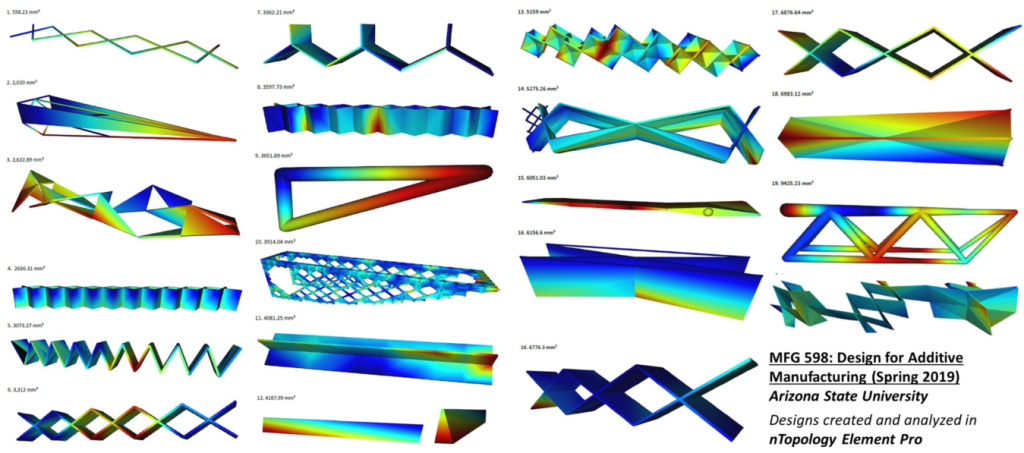
- MFG 598: Design for Additive Manufacturing (Instructor: Dhruv Bhate)
The DFAM course at ASU, first offered in the Spring of 2018, focuses on five different aspects of designing for AM: (i) an understanding of constraints imposed by AM processes and the expected properties, (ii) methods to determine what parts are good candidates for AM, (iii) topology optimization, (iv) cellular materials design, and (v) implementation realities such as the need for certification and qualification. This class also uses a flipped classroom format, with pre-recorded lectures (Figure 3), using classroom time for students to work in groups on a combination of projects and a final research poster to be delivered at the Annual SFF Symposium in August (over the past 2 years, 4 groups have made presentations at this conference, and 25 students have collectively been co-authors on a conference publication).
- MFG 598: Polymer Science in Additive Manufacturing (Instructor: Kenan Song) This course is the first of two AM courses that takes a process-structure-property approach to AM. This particular course focuses on the mechanical, thermal and electrical properties of polymers used in AM, with regard to the underlying physics and physical chemistry of polymers in melt, solution, and solid state. Topics include conformation and molecular dimensions of polymer chains in solutions, melts, blends, and block copolymers; an examination of the structure of glassy, crystalline, and rubbery elastic states of polymers; thermodynamics of polymer solutions, blends, crystallization; nanocomposites; mechanical, thermal and electrical properties in polymeric materials; lab sessions in 3D printing.
- MFG 598: Metal Additive Manufacturing (Instructor: Dhruv Bhate)
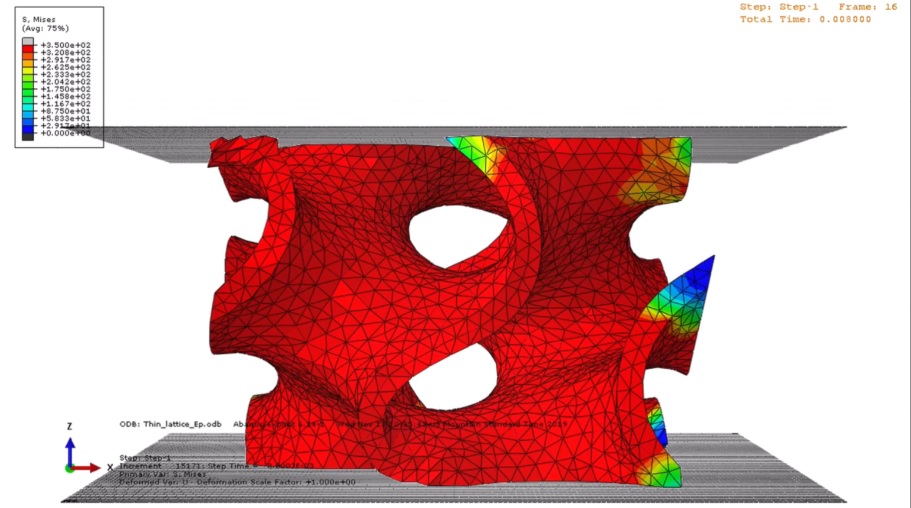
This course, offered for the first time in the Spring of 2020, provides an overview of different metal 3D printing processes, and an in-depth look at the most widely used one: the laser powder bed fusion process. For this process, the course is divided into 4 modules: process development (hands-on metal 3D printing), properties (characterization and testing), design for metal AM (use of design, and build preparation software), and process simulation (use of simulation software) – see Figure 4. This course too is taught with the flipped model, reserving classroom time for hands-on activities.

Other Related Courses
There are several courses at ASU that are not limited to AM in scope, but allow for a deeper dive into the underlying fundamentals that are relevant to AM and design for AM. Some of these courses are (this is a partial list):
- MSE 598: Introduction to Powder Processing
- EGR 598: Simulating Manufacturing Systems
- EGR 598: Manufacturing Systems Management
To learn more about these and other courses at ASU, visit ASU’s course catalog: https://catalog.asu.edu/